
Theme 2
Multiscale models
Nature works on multiple scales. Water is more than individual molecules; the economy is more than individual agents. Multiscale Models reflect the fundamental mathematical and statistical structures required to make sense of systems and data. As such, the research teams within this theme are working to develop new models and mathematical techniques, both stochastic and statistical in nature, to understand these highly complex problems.
Such an objective requires ACEMS researchers working in very different fields of mathematics and statistics to come together, share their challenges, and determine how they can each benefit the other. At one end of the spectrum are the applied statisticians who develop useful insights about how appropriate modelling strategies need to change, in order to adapt to the granularity of data measurements from the real world. At the other end are the theoretical mathematicians who use abstract and deep results in pure mathematics to shed light on concepts such as the theory of polynomials in many variables and provide advanced tools to facilitate computational algorithms. And while these two seemingly divergent fields might appear poles apart, it is the work of the applied probabilists, the mathematical physicists, the theoretical statisticians, and those mathematicians and statisticians that fall at different points of the spectrum, that bring the abstract to the real world, creating a pipeline of opportunity for new applications and discoveries.
As a result, the Multiscale Models theme research includes some of the most diverse activity within ACEMS, ranging all the way from theoretical mathematics to applied statistics.
People
Key Achievements
ACEMS AIs Brodie Lawson, Megan Farquhar, and Pamela Burrage, together with ACEMS CIs Ian Turner and Kevin Burrage, brought the theory of homogenisation to the challenging, nonlinear dynamics of cardiac electrophysiology. Homogenisation here refers to the replacement of complexly structured material with a homogenous material that exhibits (approximately) equivalent characteristics on a larger spatial scale. Describing how electrical signalling tells the heart to beat (and how dysfunctions in this process cause a range of arrhythmias), cardiac electrophysiology is well-known for long computational runtimes that inhibit simulation studies and make it infeasible to capture small-scale effects. Through homogenisation by volume averaging, the work led by Lawson demonstrates how these small-scale effects can be captured by upscaled tensors, and explores how to choose these tensors in order to best balance the errors incurred by the different approximations involved. The work led by Farquhar introduces a novel take on homogenisation, using transit times on a graph representation of the domain to choose upscaled tensors that seek to capture the actual qualities of microscale propagation. Importantly, this approach makes none of the assumptions implicit to traditional homogenisation, and so is more applicable in scenarios where those assumptions break down.
COVID-19 has severely affected the Australian tourism industry. CI Rob Hyndman, RA Mitchell O'Hara-Wild and AI George Athanasopoulos developed a new method to provide probabilistic forecasts of the road to recovery for Australian tourism. This combined state-of-the-art forecasting tools, with expert judgement, to quantify the uncertainty around tourism numbers in the next few years. This work was funded by the Austrade, and done in conjunction with Tourism Research Australia, the Australian Tourism Industry Council and the Australian Tourism Export Council. This work has been accepted for publication in the Journal of Travel Research.
In a cross-node collaboration, ACEMS PhD student Angus Lewis developed and applied new numerical techniques in applied probability theory. Angus’ research was supervised by former ACEMS Deputy Director, now ACEMS AI, Nigel Bean from the University of Adelaide, and ACEMS Director Peter Taylor from the University of Melbourne node. Mathematical models should be simple enough that they are tractable, but flexible enough so that they give a reasonable representation of the complex system being modelled. One such model is called a fluid queue which can be used to model a single performance measure of a system operating in a random environment. However, if we want to track two performance measures of a system where one depends on the other, then we need a more complex model. Enter the fluid-fluid queue which was designed to do exactly this, but at the cost of some computational tractability. Angus’ research builds computational tools for the practical analysis of the 'fluid-fluid queue' thereby enabling its use as a tool for decision making. The techniques developed approximate the local behaviour of the system on small intervals, called cells. By connecting all the cells together, this creates a global approximation to the whole system. A brand-new approximation technique was developed, called the QBDRAP approximation scheme, which is guaranteed to give feasible estimates of probabilities (which must be between 0 and 1), even for problems with discontinuous solutions (this is not guaranteed by other methods). Further, numerical evidence suggests that the QBDRAP approximation scheme has comparable performance to other state-of-the-art numerical schemes which guarantee all estimates of probabilities are between 0 and 1.
CI Phil Pollett and his group studied occupancy processes with infinitely-many sites.
Together with former ACEMS PhD student Liam Hodgkinson, who is now undertaking a postdoctoral fellowship at the University of California, Berkeley, CI Pollett studied a class of metapopulation models where there is no ceiling on the number of habitat patches that can be occupied. A “metapopulation” here refers to a regional group of connected populations of a species. The team examined the limiting behaviour as the density of patches increases. These limits are not only natural in theory, but in practice as well, as they describe models with increasing environmental fidelity.
CI Tim Garoni, together with ACEMS Research Fellow Zongzheng Zhou, ACEMS PhD student Abrahim Nasrawi and international collaborator Youjin Deng, proved significant new results on the behaviour of weakly self-avoiding walks on the complete graph in 2021. Weakly self-avoiding walks provide a mathematical model of polymers. Their study on the complete graph provided rigorous results related to the universal finite-size behaviour of statistical-mechanical models in high dimensions. Abrahim’s thesis was submitted in November 2021, and subsequently passed in February 2022. Sahil Balak joined the group in March 2021, as an ACEMS PhD student. Sahil’s project involves studying the distribution of the running time of the coupling from the past implementation of the Ising Glauber process. This project constitutes a fundamental study in mathematical physics, but also has direct consequences to the study of Markov chain Monte Carlo algorithms. Sahil’s PhD research will continue beyond ACEMS.
CI Jan de Gier produced two fundamental preprints on integrable stochastic processes in 2021, posted to the arXiv preprint server. In the first, together with ACEMS PhD student Zeying Chen and international collaborators Iori Hiki, Tomohiro Sasamoto and Masato Usui, de Gier derived the limiting current distribution for a two species asymmetric exclusion process. The asymmetric exclusion process is a discrete probabilistic model which, amongst other applications, is used to describe traffic flow along a single-lane road. In that context, the two-species generalisation corresponds to traffic consisting of two different vehicle types, e.g. cars and trucks. The second preprint describes research undertaken by de Gier with ACEMS PhD student William Mead and ACEMS AI Michael Wheeler. In this work, the researchers derived an explicit mathematical expression for the transition probability and total crossing events in the multi-species asymmetric exclusion process. In addition, as part of a University of Melbourne vacation project with student Sam Sail, de Gier produced results on the six-vertex model surface tension. The six-vertex model is a fundamental model in statistical mechanics, which models ice.
One dimensional integrable stochastic processes can be studied using algebraic methods, which are themselves in a state of constant development. One important recent development is based on the so called "shuffle algebras". In 2021, ACEMS AI Sasha Garbali, who is a recent recipient of an ARC Discovery Early Career Researcher Award, together with Paul Zinn-Justin from the University of Melbourne and international collaborator Andrei Neguţ, obtained several intriguing new connections between shuffle algebras and integrable stochastic processes. These results have been posted to the arXiv preprint server.
ACEMS PhD student Tiffany Lo, obtained impressive new results concerning random graphs in 2021. Together with ACEMS AI Andrew Barbour, the degree distribution of a randomly chosen vertex in a duplication–divergence graph was studied, under a variety of different generalisations of the basic model of Bhan. Particular attention was paid to what happens when a non-trivial proportion of the vertices have large degrees, establishing a central limit theorem for the logarithm of the degree distribution. The work was subsequently posted to the arXiv preprint archive. In addition, Lo studied local weak convergence of the linear preferential attachment random trees with additive fitness, where fitness is defined as the random initial vertex attractiveness. In particular, it was shown that the local weak limit is a weighted generalisation of the Polya point tree introduced in Berger, Borgs, Chayes and Saberi (2014). Rates of convergence in the total variation distance for several local network statistics were also given.
Finally, together with ACEMS researchers Luca Maestrini, Dorota Toczydlowska, Aishwarya Bhaskaran, Virginia He, CI Wand developed some significant advances in statistical methodology in 2021. In particular, methodology and related software was developed for generalized linear mixed model fitting and inference using Thouless-Anderson-Palmer adjustments to Gaussian variational approximation. In addition, asymptotic normality results were obtained for maximum likelihood estimators of dispersion parameters in generalized linear mixed models. Fast variational Bayes approaches to generalized additive model selection and generalized additive mixed model selection were also developed. In December 2021, ACEMS PhD student Aishwarya Bhaskaran presented results on asymptotics for generalized linear mixed models at the annual J.B. Douglas Postgraduate Awards Day.
CI Peter Taylor continued his collaboration with CI de Gier, AI Rhys Bowden and international collaborator Tony Krzesinski on understanding the dynamics of blockchain structures. The focus of their work in 2021 was on blockchain systems with a fast mining rate compared to their communication rate. Such systems spend far less time in consensus that conventional slow mining blockchains. In fact a better description of their data structures would be a `blocktree’ rather than a blockchain. In exciting developments, the researchers proved that consensus in such a structure, while rare, is still positive recurrent. Furthermore, they conjectured that the lack of consensus in a blocktree will be confined to a region that lies within a bounded distance from the highest leaf in the tree. This means that such a data structure can still function provided we rely on blocks that are at a sufficient depth.
With PhD student Punya Alahakoon and colleague James McCaw, CI Peter Taylor studied methods for estimating infection parameters in hierarchical Bayesian models for epidemics with replenishment of susceptibles. They reported the results in a paper published in Epidemics where the additional went on the estimate the probability of epidemic fadeout in the first trough after the peak of infection.
PhD students Jiesen Wang and ChenChen Xing, AI Mark Fackrell and CI Peter Taylor continued their work on strategic queueing models. In a paper published in Queueing Systems they derived Nash equilibrium threshold strategies for customer joining probabilities at a feedback queue and observed that interesting and paradoxical behaviour can occur in which all customers can be worse off when the reward for service is increased and where customers are given the opportunity to renege at the time points where feedback occurs.
PhD student Behrooz Niknami and CI Peter Taylor continued their study of stochastic matching models with `benevolent nodes’, that is customer types that can match other customers but don’t themselves remain in the system if they are not matched. The team extended recent work that demonstrated that such models have product-form invariant measures to this new class. They also pointed out that limit order books have the structure of such a stochastic matching model, albeit with a different queueing discipline, in which customers are matched with the best available match rather than the one that arrive earliest, and explored the ramifications of this observation. Behrooz will submit his thesis early in 2022.
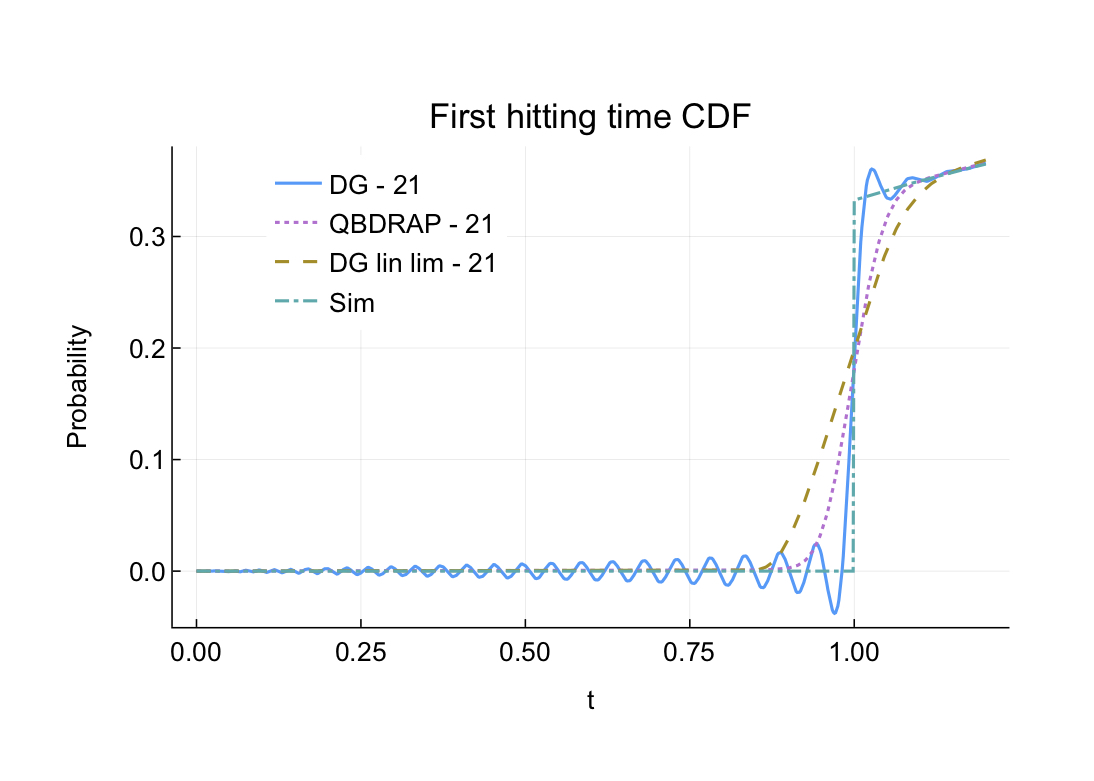
Comparison of the performance of the QBDRAP approximation scheme with previous methods

Example of dramatic mathematical simplification discovered by CI Wand and his group.
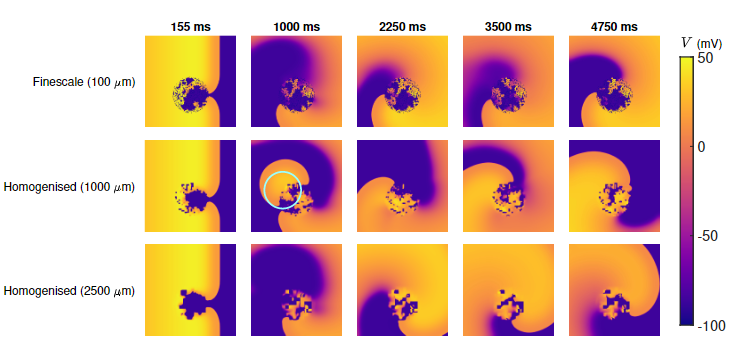
Careful calculation of upscaled conductivity tensors allows for the nonlinear dynamics of arrhythmia to be captured in far less simulation time.
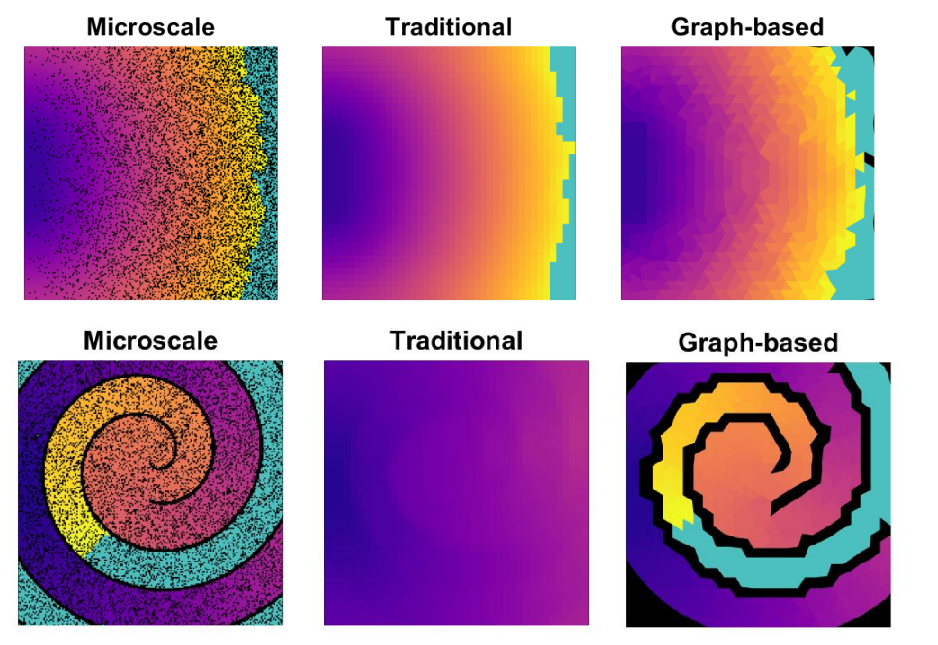
The use of a novel graph-based homogenisation idea allows for the effects of more intricate structures of obstruction to be appropriately captured in upscaled models.

Animation of the six-vertex model surface tension
In January 2020 there was a glaring gap in maximum likelihood theory for a major class of statistical models: generalized linear mixed models. By late 2021 ACEMS doctoral candidate, Aishwarya Bhaskaran, had the makings of a thesis which closed this gap.
ACEMS CI Matt Wand, UTS